Risk is defined differently depending on the (scientific) discipline. In general, the term “risk” denotes the potential loss of something of value, e.g. health or an intact environment or simply your purse. A risk exists only if hazard and exposure occur together.
In toxicology, the term risk describes the function of the probability of “exposure” to the “hazard” potential a given material exhibits:
RiskTox = f{exposure; hazard}.
In contrast to the simplified explanation given in the basics article Do nanomaterials harbour risks? a closer look shows that the definition of risk as a product of two factors does not correctly describe risk, because the relation of the two “factors” exposure and hazard may be not linear depending on the height of exposure.
It can also be seen as the area of the intersection of “Exposure” and “Hazard” meaning that there is only a risk to humans, animals or the environment, if there is an exposure to a hazardous material.

Left: virtually no risk, when exposure is negligible. Middle: Risk is described by the overlapping area of exposure and the hazard potential of the given material. Right: virtually no risk, when exposed to a negligible hazard. © DaNa-Team.
Risk assessment of nanomaterials
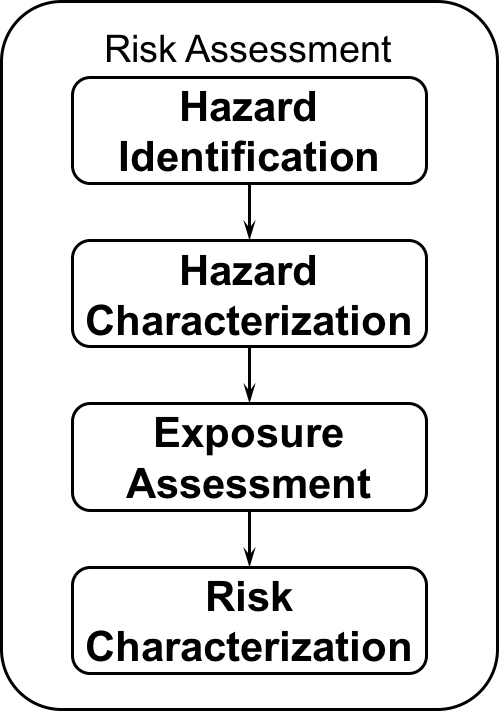
Schematic sketch of risk assessment © Brune, H. et al. (2006). Nanotechnology – Assessment and Perspectives, Vol 27, Springer Verlag, Berlin. ISBN 978-8184890518
Risk assessment of nanomaterials is the second step of any risk analysis after having characterised a certain risk. Assessing the risk will deliver facts for a reasonable risk management.
For nanomaterials, chemical risk assessment is very often relevant. Here, two points need to be addressed. First, it is mandatory to identify and examine a potential hazard of the material under controlled conditions e.g. in the lab. The second mandatory point is to measure and quantify exposure, i.e. the amount of material, which comes into contact with humans, animals or the environment, respectively. On the basis of these first two steps a specific risk can be characterized and a decision has to be made about the height of the risk for each exposure scenario (traffic light scheme).
Exposure assessments of nanomaterials are still under way and far from being complete due to the lack of available exposure measurement methods. Reliable routine airborne exposure measurement methods are not available, although exposure measurements of nanomaterials at the workplace and/or in the environment are urgently needed. Moreover, the biological and environmental distribution pathways of nanomaterials are largely unexplored but the situation improves with new publications [1-3].
Whether there is a potential risk of nanomaterials cannot be answered in one simple statement. To give an answer the varying hazard potentials of the different nanomaterials and the variance in possible exposure scenarios have to be considered for a specific situation.
Currently, risk assessment of manufactured nanomaterials is done on a case-by-case basis. But testing of all existing nanomaterial variants is not feasible. One solution to overcome this problem is grouping of nanomaterials, which is in the focus of projects such as nanoGRAVUR or NanoToxClass and is explained below in some detail.
Categorization of Nanomaterials
Categorization or grouping means the basic mental process of arranging things etc. into classes or categories depending on their intrinsic properties or activities. Grouping and categorization of nanomaterials or nanoobjects has become one priority goal to regulate the fast development of these materials.
Given the broad range of different possibilities to change the properties of manufactured nanomaterials such as size, shape or coating risk assessment is a laborious, time- and cost-intensive process. Testing all nanomaterial variants for all possible endpoints is not feasible. One solution to overcome this problem is grouping and categorization of nanomaterials [4-6]. This is why the European Commission and the Federal German Ministry of Education and Research (BMBF) fund a project NanoToxClass to work out and establish grouping and categorization strategies for nanomaterials according to toxicity and biological effects to support risk assessment of nanomaterials.
The definitions for grouping and categorization of nanomaterials may be based on those for chemicals [1], but the test procedures and definitions cannot be translated directly from chemicals to nanomaterials. A translation is urgently needed to facilitate the development of nanotechnological applications while ensuring safe applications in parallel. The current state of knowledge on the hazard of nanomaterials towards protected assets is so complex that the BMBF-funded project nanoGRAVUR made it its central objective to develop different criteria catalogues for a grouping of nanomaterials according to the respective potentials for exposure, hazard and risk.
As a consequence, grouping of substances and read-across [5] are one of the most commonly used alternative approaches for filling data gaps in registrations submitted under REACH [1].
The last step in risk analysis “Risk management” is described in the cross-cutting text Risk Management of Nanomaterials.
Literature
- Hansen, S F et al. Nanotechnology and human health: Scientific evidence and risk governance: Report of the WHO expert meeting 10–11 December 2012, Bonn, Germany. World Health Organization ((PDF, 906 KB )
- Coll, C et al (2015) Nanotoxicology 10 (4), 436-444
- Wang, Y et al. (2016) Sci. Total Environ 545-546, 67-76
- Walser, T., Studer, C. (2015) Regul. Toxicol. Pharmacol. 72, 569-571
- ECHA: Grouping of substances and read-across approach ((PDF, 400 KB )
- ECHA (2016): Usage of (eco)toxicological data for bridging data gaps between and grouping of nanoforms of the same substance. European Chemicals Agency, Helsinki, Finland, Practical Guide ((PDF, 922 KB )
 >
>